Model Checking is part of the Formal Methods which address formal specification, formal development, formal verification and theorem provers. Model Checking belongs to the formal verification and provides a complete mathematical proof to verify your system-under-test.
BTC EmbeddedPlatform uses the model checking technology for structural test data generation to achieve full code coverage, for formal verification to prove if a formalized requirement can ever be violated and for test case generation for formalized requirements.
Now let me introduce you to my colleague Dr. Karsten Scheibler. He is one of our experts for the topics of model checking in our Innovation & Technology department and inventor and developer of our iSAT3 model checking engine.
Wolfgang: Hey Karsten, thanks for joining in this blog article. How did you end up with model checking?
Karsten: Hi Wolfgang, basically, this came through my doctoral studies which had model checking as topic.
Wolfgang: You have many years of experience with model checking. You even designed and programmed a model checker on your own! How would you explain what a model checker is to someone who has never heard of it?
Karsten: As the name suggests model checking is about checking properties of a model. Thus, a model checker is a tool to perform such checks. But this brings up the question what a model is. Instead of considering the system of interest directly, an abstraction of the system (a so-called model) is analyzed. Such a model usually consists of a set of states and a description (a so-called transition relation) which specifies how the model changes its state when time passes. In many cases, only discrete points in time are considered. Thus, time increments in steps. Hence, when performing such a step and going from time point t to t+1, the transition relation specifies the state of the model in t+1 depending on its state in t.
OK, this sounds still very abstract. Do you have an example?
Let me illustrate this with a traffic light. When creating a model for a traffic light, the model states correspond to all possible combinations of enabled and disabled green, yellow and red lights – while the transition relation describes which lights will be turned on or off when performing a time step (such a time step could be, e.g., one second). Furthermore, additional inputs might influence the behavior of the system in a nondeterministic way. In this example this might be an additional button at the traffic light to get a green light for a pedestrian crossing. Such inputs have to be considered in the transition relation as well. When checking this traffic light model an interesting property might be: “Is it impossible to enter a state with all green lights being turned on”. Let’s denote a state which violates a property a bad state.
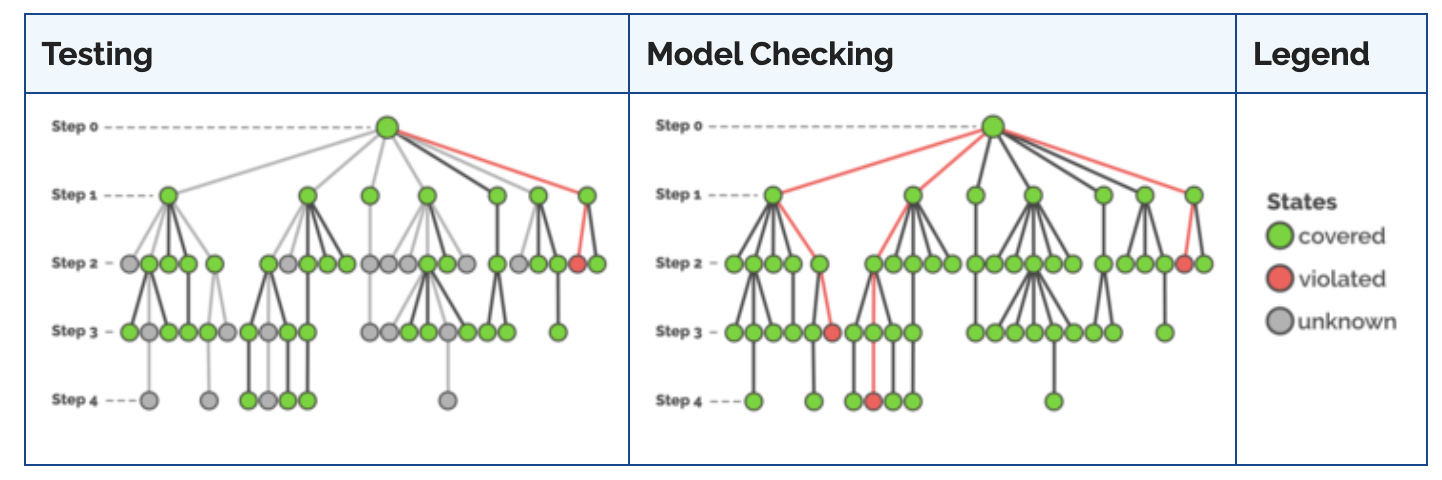
While in a classical test approach, even with many test cases, only a subset of all possible states can be covered, Model Checking will provide a complete analysis of all possible states.
So bad state means that the property I want to verify is violated?
Yes! Informally, a model checker searches for reachable bad states. More formally, when checking a property, the task of a model checker is to determine whether there exists a sequence of valid state transitions starting in a given initial state and ending in a bad state (e.g., a state with all green lights being turned on). If such a sequence exists, the property is violated – if there is no such sequence, the property is proven.
You have spoken about properties and bad states but what exactly does the model checker do?
Basically, a model checker keeps track of the set of reachable states – let’s call this set R. At the beginning R is initialized with the given initial states. Now, the model checker iteratively performs a time step and adds all states to R which the system might transition into. The model checker stops if either a bad state is added to R (property violated), or R stays constant when performing a time step (property proven).
You talked about a model which abstracts the system of interest, but how does such a model look like when considering automotive software?
In fact, software can be understood as a formal description of a system. Thus, in this respect software needs no abstracting model – or in other words: the software is already the model we want to check properties on. Let’s consider a small C program:
static int s = 0;
void f(int i1, int i2, int i3) { if (i1 + i2 + i3 == 12345) s++;}
In this program we have a global variable s and a function f() with three parameters i1, i2 and i3. The global variable s can be understood as the state of the program while the function f() can be seen as the transition relation because f() might change the program state each time it is called. Similarly, the parameters of f() correspond to inputs.

Now, one might ask if it is possible to reach a program state with s != 0 – or in terms of a model checker: we want to check the property: “s is always 0”. For a programmer it is obvious that this property will be violated, e.g., with i1 = 0, i2 = 0 and i3 = 12345. Hence, these values form a stimuli vector reaching the statement s++. While a human has no problem to find this stimuli vector, random automatic test generation approaches will need a long time as they simply assign random values to i1, i2 and i3. Thus, these approaches have to try many value combinations to find one which satisfies the if condition.
This sounds like a very comprehensive task to find this specific combination of values. Random automatic test generation seems not to be the best choice here. How does a model checker handle this task?

Let’s denote all possible value combinations of i1, i2 and i3 as the search space. While random automatic test generation approaches navigate erratically through the search space, a model checker is more systematic and tries to find shortcuts in the search space. Depending on the underlying technique used by the model checker this could mean, e.g.:
(1) The model checker assigns values step-by-step and tries to deduce further values after each assignment. Regarding the aforementioned small C program this means, after assigning values for i1 and i2 the model checker calculates the right value for i3 in order to satisfy the if condition. Furthermore, if the model checker finds out that one value combination does not work, it tries to generalize this knowledge to other value combinations as well. Thus, in this context a shortcut stands for a reduction of the number of explicitly tried value combinations.
(2) The model checker uses a special data structure to represent the set of states. If it is possible to keep this data structure compact, then operations can be executed efficiently. But depending on the structure of the state set, the size of this special data structure might exceed the available memory. Hence, in this context a shortcut stands for a compact representation of the state set.
But does this not mean, that we have a huge search space that needs to be handled?
Yes, that’s why model checkers try to prune the search space as much as possible. One should keep in mind that a property is only proven if the property holds for all value combinations in the search space. Hence, either all value combinations in the search space are tested explicitly (which is already infeasible with a search space of size 2^64, e.g., two 32-bit integers) or shortcuts are used.
The enumeration above might suggest that there are only two kinds of shortcuts – but this is misleading. Basically, a shortcut exploits the characteristics of a specific operation. Thus, there are no generic shortcuts and not all model checkers use the same kinds of shortcuts. This also explains why one model checker might work well on a specific program while another model checker might not terminate in reasonable time on the same program.
What happens, if the model checker cannot find a shortcut?
Depending on the type of model checker this could mean that (1) the model checker has to test many value combinations explicitly, or (2) the special data structure for the state set exceeds the available memory. Usually, model checkers always find shortcuts – but it might happen that the shortcuts are simply not good enough. In such cases a model checker does not terminate in reasonable time or runs out of memory.
I saw that model checkers can address and support different use cases in testing. They can be used to generate structural test data reach full coverage for a model and code, proof that a formal requirement can never be violated, or even generate requirements-based test cases from a formal requirement. How is it possible that a model checker can deliver results for these use cases?
The magic here lies in the preparation – each use case is prepared in such a way that the model checker has to find a stimuli vector. For example, if a program P1 (usually your system-under-test) should be checked regarding a formal requirement, then the formal requirement is translated into a program P2 which is then merged with P1 into a new program P3. Please keep in mind, P2 is constructed in such a way that a dedicated variable is set to 1 if the requirement is violated and remains 0 otherwise. Now, the task of the model checker is to find a stimuli vector in P3 to reach the statement which sets the dedicated variable to 1. If such a stimuli vector exists, the formal requirement is violated – otherwise the requirement is fulfilled and there is no input combination possible to violate the requirement.
All these results sound great! However, are there also some limitations and challenges using this technology?
As mentioned, model checkers differ in the kinds of shortcuts they are using – while one model checker might work well on a specific program another model checker might not terminate in reasonable time on the same program. This can be mitigated by using different model checkers. Furthermore, with today’s multicore CPUs it is also possible to start multiple model checkers in parallel. Additionally, good preprocessing is key to decent performance – even the best model checker will perform poorly if the problem to be solved is encoded badly.
We are at the beginning of 2021. Do you think, there will be a breakthrough in this technology or will it be replaced by another approach that is probably more efficient and can deliver comparable results?

I think model checking is here to stay. Furthermore, I believe we will see further improvements in the future – for example, due to a better preprocessing. Additionally, what feels like a breakthrough for a user of model checking might be in fact just an improved combination of existing techniques within a model checker. Hence, shortcuts are and will be your best friends!
Thanks to you Karsten for all these great insights in this interesting and powerful technology. Have a nice day and maybe we can see you soon again here.
Conclusion
Model checking is a powerful technology that was developed since the mid-eighties by a strong academic community. For over 20 years, BTC Embedded Systems has deep relationships with this community and we have brought many innovations which has made the technology available to embedded software developers around the globe. Please, also have a look at the article from my colleague Dr. Tino Teige about “The Power of Focus” that shows how much can be reached if this technology is adapted in the right way to a specific domain like automotive.
The bottom-line is, model checking adds a great value in your project for different use cases including robustness, drive-to-state, boundary value analysis and formal verification, to name a few. It gives the user mathematical proven confidence for the checked properties, while helping to be ISO 26262 compliant – especially for ASIL C and D projects. Furthermore, since most of these analyses do not need human interaction, they can be fully automated in your testing workflow reducing the workload on the testing team.



